正多角形と私

　私にとって労作展は、 色んな世界に目を向けることが出来る場だと思った。 労作展は普通部の志望理由の１つでもあった。 私は小学校時代、 いやそれより前かもしれないが、 算数という教科が、 たまらなく好きだった。 計算により出てくる答えがただ１つぴったりになることも快感だった。 小学校で一番好きだった算数のジャンルは 「数と計算、 式」 であった。 それが得意だと他の事を勉強することも好きになっていった。 そんな算数とももうお別れ。 中学１年生になり、 新しい教科 「数学」 が始まったのである。 当時は算数と数学の違いをあまり知らなかった。 数学と算数の違い、 それは 「文字における一般化」 （抽象化するという意味である） である。 この考え方も、 私が３年間数学科で労作展をする上で、 とても大事であった。
　中学１年生。 受験が終わった直後である。 その時は何をしていたのだろうか。 今はあまり覚えていない。 労作展は、 正多角形の面積から円周率を計算してみるというものだった。 半径１㎝ の内接する （円にすっぽり入る） 正多角形と外接する （円をすっぽり入れる） 正多角形を２つ書いて円周率の範囲を絞り込んでいくというものであった。 正多角形をより細かくしていく （辺の数を増やす） ことで、 誤差がどんどん少なくなっていく仕組みだ。 この手法は古代ギリシャの数学者アルキメデスも行っていたものだ。 私は小数点以下10桁を求めることに成功した。 この時私は最後に円は辺の数が無限である正多角形であるということを結論として出した。 そしてこれは３年生の労作展へと受け継がれた。
　中学２年生。 この頃は真面目に勉強していたのだろう。 クラス替えがあり、 人数も増え40人になった。 ２年生の労作展では、 色々な宝くじの１枚あたりの還元率 （価値） を比較するというものだった。 宝くじは当たり前のことだが１枚の価格より還元率は少ない。 しかし、 どれくらい少ないのかは、 各宝くじによって違っている。 還元率の求め方はざっくり言うと１等が当たる確率×１等の当選金額＋２等が当たる確率×２等の当選金額＋３等の…という値を１枚の宝くじの値段で割ると求められる。 また、 宝くじは２種類あり、 ①自分で還元率を上げることが出来ない宝くじと②自分次第で還元率を上げることができる宝くじがある。 ①にはジャンボ宝くじなどが、 ②にはナンバーズなどが含まれる。 労作展では過去1000回分の統計から考えて還元率をできるだけ上げるということをした。 約47％から約52％まで上げることが出来た。
　中学３年生。 労作展ももう最後である。 中学校に入学してからしばらく経っているはずなのに労作展と聞くと新しく感じた。 今年は、 正多角形の面積について研究した。 これは１年生の労作展のテーマとかなり近い。 ３回しかない貴重な場である労作展だが、 テーマを被せるなんて勿体ないと思っていた。 しかしそれでも正多角形の研究がしたかった理由は、 １年生の時結局何が言いたいの？という風に終わってしまったので、 その続きをやりたいと思ったからである。
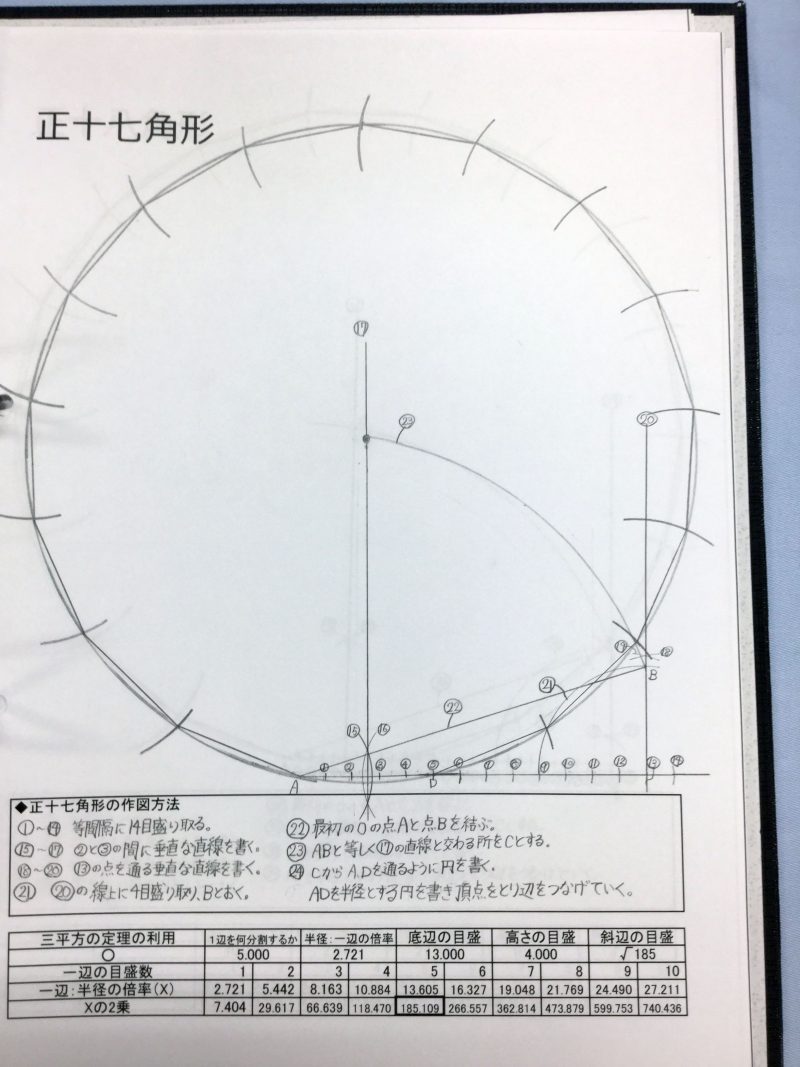
　３年生では、 定規とコンパスを決められた規則に従って使い、 正多角形から徐々に辺の数を増やしていき、 正二十四角形まで作図した。 作図すると正多角形を２種類に分類することが出来た。 作図できる正多角形と作図できない正多角形である。 前者には、 正三角形、 正五角形などが、 後者には、 正七角形、 正十一角形などが属する。 理論上作図できない正多角形もあるので、 その場合は１辺の長さと外接円の半径の長さの比を計算し、 できるだけ正確に作図した。 またその作図した正多角形の面積を求めることにした。 面積を求める方法が難しかったので、 簡単に求められる方法を考えた。 正多角形の性質を確認していた時に私は閃いた。 「円周率のように各正多角形には面積を求めるための定数が存在する」 と考えたのだ。 それを 「相対面積Ｓ係数」 と名付け、 それぞれの正多角形の相対面積Ｓ係数を求めた。 これにより今までは関数電卓が必要だった計算がはるかに楽になった。
　３年間で一番苦労したことは、 制作日誌である。 技術や美術の制作日誌は分かり易く簡単だが、 数学はそうもいかないのである。 数学でとても重要となる過程が抜けていると元も子もないそうだ。 労作展は、 数学の新たな世界に目を向ける良い機会だった。 労作展は普通部生ならきっと永遠に忘れることはなく、 未来に語り継げられるだろう。